Distance Formulas

In the Machine Learning literature very often we can see the terms of distance computing. Some of the machine learning algorithms built upon this formulas such KNN, clustering etc.

Here we are going to briefly see several types of the distance formulas which used by the machine learning algorithms.

Euclidean Distance

According to Wikipedia;

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" straight-line distance between two points in Euclidean space. With this distance, Euclidean space becomes a metric space. The associated norm is called the Euclidean norm. Older literature refers to the metric as a Pythagorean metric. A generalized term for the Euclidean norm is the L2 norm or L2 distance.

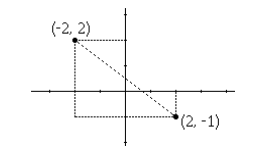
Briefly, Euclidean distance is the straight line distance between two points which are in the Euclidean Space.

Distances between two points according to Euclidean Distance Formula is;

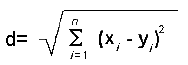
Manhattan Distance

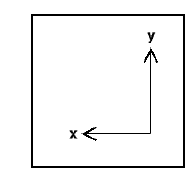
The Manhattan distance formula computes the distance between the points by assuming that grid-like path as the distance between the points.

Distance between two points according to Manhattan Distance Formula is;

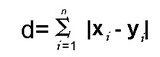
Cosine Distance

Cosine distance formulate computes angular cosine distance between the points.

Distance between two points according to Cosine Distance Formula is;

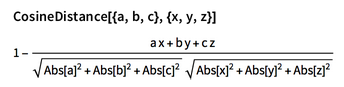
Thanks for reading.